Advertisements
Advertisements
Question
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
Options
100 m
120 m
25 m
200 m
Solution
Given: Vertical stick 20m long casts a shadow 10m long on the ground. At the same time a tower casts the shadow 50 m long on the ground.
To determine: Height of the tower
Let AB be the vertical stick and AC be its shadow. Also, let DE be the vertical tower and DF be its shadow.
Join BC and EF.
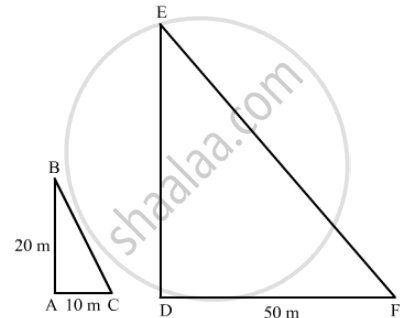
In ΔABC and ΔDEF, we have
`∠A=∠D=90^o`
`∠C=∠F`
`Δ ABC ∼ Δ DEF`
We know that in any two similar triangles, the corresponding sides are proportional. Hence,
`(AB)/(DE)=(AC)/(DF)`
`20/(DE)=10/50`
`DE=100m`
Hence the correct answer is option `a`.
APPEARS IN
RELATED QUESTIONS
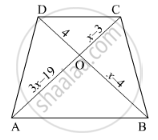
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
State Pythagoras theorem and its converse.
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
