Advertisements
Advertisements
Question
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
Options
18 cm
20 cm
12 cm
15 cm
Solution
Given: ΔABC and ΔDEF are similar triangles such that DE = 3cm, EF = 2cm, DF = 2.5cm and BC = 4cm.
To find: Perimeter of ΔABC.
We know that if two triangles are similar then their corresponding sides are proportional.
Hence, `(AB)/(DE)=(BC)/(EF)=(CA)/(FD)`
Substituting the values we get
`(AB)/(BC)=(DE)/(EF)`
`(AB)/4=3/2`
`AB=6cm`..................(1)
Similarly,
`(CA)/(BE)=(DF)/(EF)`
`(CA)/4=2.5/2`
`CA=5cm`
Perimeter of Δ ABC = AB+BC+CA
= 6+4+5
= 15 cm
Hence the correct option is `d`
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
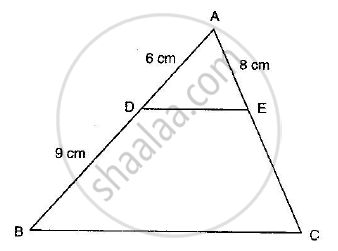
In the adjoining figure, find AC.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
