Question

In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then

Options

• AQ² + CP² = 2(AC² + PQ²)

• 2(AQ² + CP²) = AC² + PQ²

• AQ² + CP² = AC² + PQ²

• \[AQ + CP = \frac{1}{2}\left( AC + PQ \right)\]

Answer 1

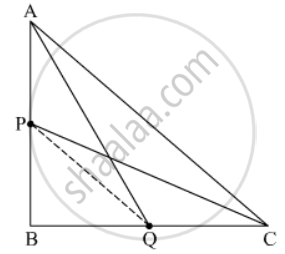
Applying Pythagoras theorem,

In ΔAQB,

\[{AQ}^2 = {AB}^2 + {BQ}^2\] .....(1)

In ΔPBC

`CP^2=PB^2+BC^2`..............(2)

Adding (1) and (2), we get

\[{AQ}^2 + {CP}^2 = {AB}^2 + {BQ}^2 + {PB}^2 + {BC}^2 \]....(3)

In ΔABC,

`AC^2=AB^2+BC^2`....(4)

In ΔPBQ,

\[{PQ}^2 = {PB}^2 + {BQ}^2\].........(5)

From (3), (4) and (5), we get

\[{AQ}^2 + {CP}^2 = {AC}^2 + {PQ}^2\]

We got the result as `c`