Advertisements
Advertisements
Question
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

Solution
We have, `Δ ABCD ∼ Δ PQRS `
So the ratio of the sides of the quadrilaterals will be proportional to each other.
`(AB)/(PQ)=(BC)/(QR)=(CD)/(RS)=(DA)/(SP)`
Therefore put the values of the known terms in the above equation to get,
`20/7=16/x=50/y=50/(3z)`
On solving these simultaneous equations, we get
`x= 28/5`
`y=35/2`
`z=35/6`
APPEARS IN
RELATED QUESTIONS
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.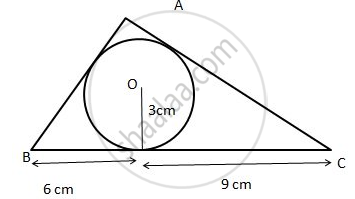
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
In the given figure, the value of x for which DE || AB is
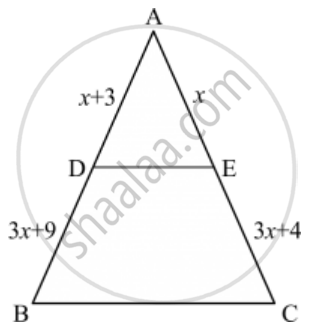
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
