Advertisements
Advertisements
Question
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
Options
9 cm
10 cm
6 cm
8 cm
Solution
Given: In Δ ABC and ΔPQR
`Δ ABC ∼ Δ PQR`
`Ar (Δ ABC) = 4Ar (Δ PQR)`
`BC=12 cm`
To find: Measure of QR
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`(Ar(Δ ABC))/(Ar(Δ PQR))=(BC)^2/(QR)^2`
`(4Ar(Δ ABC))/(Ar(Δ PQR))=12^2/(QR^2)`(Give Ar(Δ ABC)=4Ar (Δ PQR))
`4/1=12^2/(QR^2)`
`2/1=12/(QR)`
Hence the correct answer is `c`
APPEARS IN
RELATED QUESTIONS
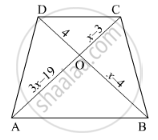
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
