Advertisements
Advertisements
प्रश्न
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
विकल्प
9 cm
10 cm
6 cm
8 cm
उत्तर
Given: In Δ ABC and ΔPQR
`Δ ABC ∼ Δ PQR`
`Ar (Δ ABC) = 4Ar (Δ PQR)`
`BC=12 cm`
To find: Measure of QR
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`(Ar(Δ ABC))/(Ar(Δ PQR))=(BC)^2/(QR)^2`
`(4Ar(Δ ABC))/(Ar(Δ PQR))=12^2/(QR^2)`(Give Ar(Δ ABC)=4Ar (Δ PQR))
`4/1=12^2/(QR^2)`
`2/1=12/(QR)`
Hence the correct answer is `c`
APPEARS IN
संबंधित प्रश्न
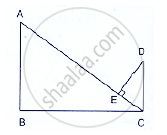
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
