Advertisements
Advertisements
प्रश्न
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
उत्तर
The ratio of the areas of two similar triangles is equal to the ratio of the square of any two corresponding sides.
`\text{(Area of triangle)}/\text{(Area of larger triangle)}=\text{(Corresponding side of smaller triangle)}^2/\text{(Corresponding side of larger triangle)}^2`
`\text{(Area of triangle)}/\text{(Area of larger triangle)}= 2^2/3^2`
`48/\text{(Area of larger triangle)}= 4/9`
Area of larger triangle =`(48xx9)/4`
Area of larger triangle = 108
Hence the area of the larger triangle is ` 108 cm^2`
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
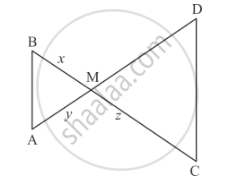
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
In the given figure, if ∠ADE = ∠ABC, then CE =