Advertisements
Advertisements
प्रश्न
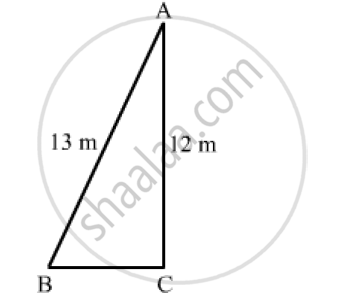
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
उत्तर
Let AB and AC be the ladder and height of the building.
It is given that :
AB = 13 m and AC = 12 m
We need to find distance of the foot of the ladder from the building, i.e, BC.
In right-angled triangle ABC, we have:
`AB^2=AC^2+BC^2`
⟹ `BC=sqrt(13^2-12^2)`
=`sqrt(169-144)`
`=sqrt25`
=5 m
Hence, the distance of the foot ladder from the building is 5 m
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
