Advertisements
Advertisements
प्रश्न
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
विकल्प
108 cm2
96 cm2
48 cm2
100 cm2
उत्तर
Given: In Δ ABC and Δ DEF
`Δ ABC ∼ Δ DEF`
`Ar (ΔABC)=54 cm^2 `
`BC=3cm`and `EF=4cm`
To find: Ar(Δ DEF)
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`(Ar(ΔABC))/(Ar(ΔDEF))=(BC)^2/(EF)^2`
`(54)/(Ar(ΔDEF))=3^2/4^2`
`(54)/(Ar(ΔDEF))=9/6`
`(54)/(Ar(ΔDEF))= (16xx54)/9`
`Ar(ΔDEF)=96 cm^2`
Hence the correct answer is `b`
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
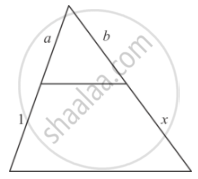
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

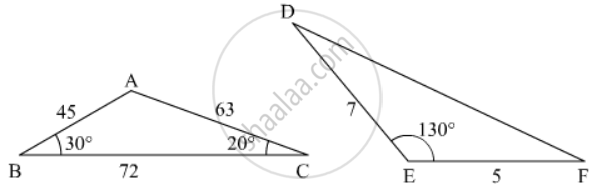
In the given figure the measure of ∠D and ∠F are respectively
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB2 + BC2 + CA2 =
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
