Advertisements
Advertisements
प्रश्न
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
उत्तर

We have,
Height of girl = 90 cm = 0.9 m
Height of lamp-post = 3.6 m
Speed of girl = 1.2 m/sec
∴ Distance moved by girl (CQ) = Speed × Time
= 1.2 × 4 = 4.8m
Let length of shadow (AC) = x cm
In ΔABC and ΔAPQ
∠ACB = ∠AQP [Each 90°]
∠BAC = ∠PAQ [Common]
Then, ΔAB ~ ΔAPQ [By AA similarity]
`therefore"AC"/"AQ"="BC"/"PQ"` [Corresponding parts of similar Δ are proportional]
`rArrx/(x+4.8)=0.9/3.6`
`rArrx/(x+4.8)=1/4`
⇒ 4x = x + 4.8
⇒ 4x – x = 4.8
⇒ 3x = 4.8
`rArrx=4.8/3=1.6` m
∴ Length of shadow = 1.6m
APPEARS IN
संबंधित प्रश्न
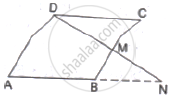
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
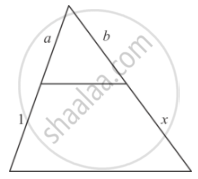
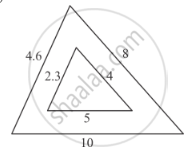
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In the given figure, DE || BD. Determine AC and AE.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
