Advertisements
Advertisements
प्रश्न
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
उत्तर
GIVEN: DE is parallel to BC, AD = 1cm and BD = 2cm.
TO FIND: Ratio of ΔABC to area of ΔADE
According to BASIC PROPORTIONALITY THEOREM, if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
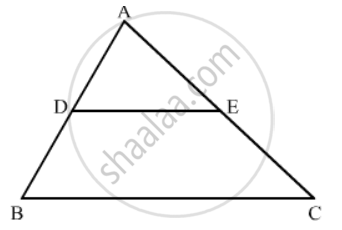
In ΔABC, DE || BC.
`(AD)/(AB)=(AE)/(AC)`
`1/(2+1)=(AE)/(AC)`
`⇒ (AE)/(AC)=1/3`
So
`(ar(Δ ABC))/(ar(Δ ADE)``=((AC)/(AE))^2`
`=(3/1)^2`
`=9/1`
APPEARS IN
संबंधित प्रश्न
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
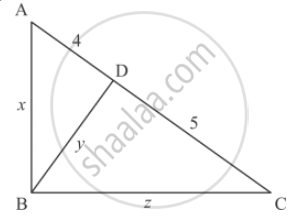
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
