Advertisements
Advertisements
प्रश्न
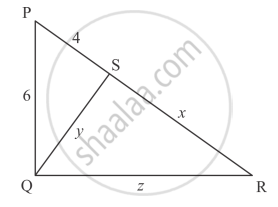
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
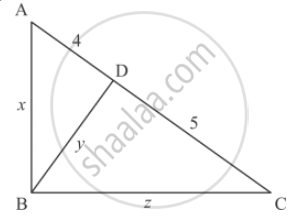
उत्तर
Δ ABC is right angled triangle right angled at B
`AB^2+BC^2= AC ^2`
`x^2+z^2=(4+5)^2`
`x^2+z^2=9^2`
`x^2+z^2=81`...............(1)
Δ BAD is right triangle right angled at D
`BD^2+AD^2=AB^2`
`y^2+4^2=x^2`
`y^2+16=x^2`
`16=x^2-y^2`...............(2)
Δ BDC is right triangle right angled at D
`BD^2+DC^2=BC^2`
`y^2+25=z^2`
`25 = z^2-y^2`..................(3)
By canceling equation (1) and (3) by elimination method, we get
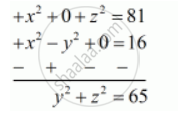
y canceling and by elimination method we get
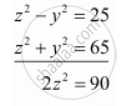
`z^2=90/2`
`z^2=45`
`z=sqrt45`
`z=sqrt(3xx3xx5)`
`z=3sqrt5`
Now, substituting `z^2=45` in equation (iv) we get
`y^2+z^2=65`
`y^2+45=65`
`y^2=65-45`
`y^2=20`
`y = sqrt20`
`y=sqrt(2xx2xx5)`
`y=2sqrt5`
Now, substituting `y^2=20` in equation (ii) we get
`x^2-y^2=16`
`x^2-20=16`
`x^2=16+20`
`x^2=36`
`x=sqrt36`
`x=sqrt(6xx6)`
`x = 6`
Hence the values of x, y, z is `6,2sqrt5,3sqrt5`
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
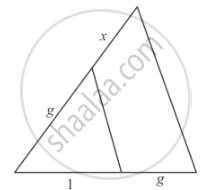
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
