Advertisements
Advertisements
प्रश्न
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
उत्तर
We have the following figure.
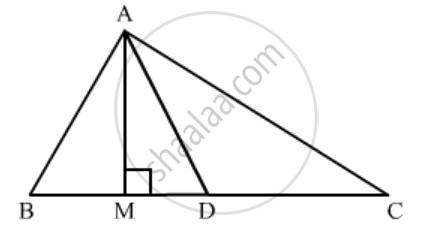
Since triangle ABM and ACM are right triangles right angled at M
`AB^2=AM^2+BM^2`.....(1)
`AC^2=AM^2+CM^2`.....(2)
Adding (i) and (ii), we get
`AB^2+AC^2=2AM^2+BM^2+CM^2`
Since in triangle ADM we have
`AD^2=DM^2+AM^2`
So,
`AB^2+AC^2=2(AD^2-DM^2)+BM^2+CM^2`
`=2AD^2-DM^2+BM^2+CM^2`
`=2AD^2-DM^2+BM^2+CM^2+2BMxxCM-2BMxxCM`
`= 2AD^2-2DM^2+(BM+CM)-2BMxxCM`
BM + CM = BC
So,
`AB^2+AC^2=A2AD^2-2DM^2-2MBxxCM+BC^2`
`AB^2+AC^2=2AD^2-2DM62-2MBxxCM+4CD^2`
`=2AD^2+4CD^2-2DM^2-2(CD+DM)(CD-DM)`
`=2AD^2+4CD^2-2DM^2-2CD^2+2CDxxDM-2DMxxCD+2DM^2`
`= 2AD^2+2CD^2`
Hence proved `AB^2+AC^2=2AD^2+2CD^2`
APPEARS IN
संबंधित प्रश्न
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
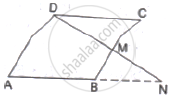
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
State SAS similarity criterion.
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
