Advertisements
Advertisements
प्रश्न
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
उत्तर
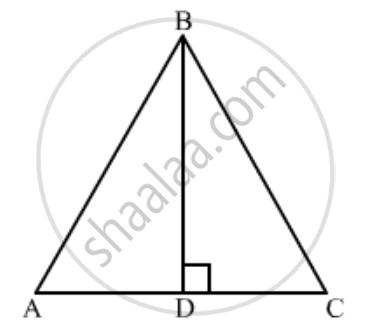
Since Δ ADB is right triangle right angled at D
`AB^2=AD^2+BD^2`
Substitute `AB=AC`
`AC^2 =AD^2+BD^2`
`AC^2=(AC-DC)^2+BD^2`
`AC^2=AC^2+DC^2-2AC.DC+BD^2`
`2AC.DC=AC^2-AC^2+DC^2+BD^2`
`2AC.DC=DC^2+BD^2`
Now, in Δ BDC, we have
`CD^2+BD^2=BC^2`
Therefore , `2AC.DC = DC^2+BD^2`
`2AC.DC=BC^2`
Hence proved.
APPEARS IN
संबंधित प्रश्न
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
State AAA similarity criterion.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
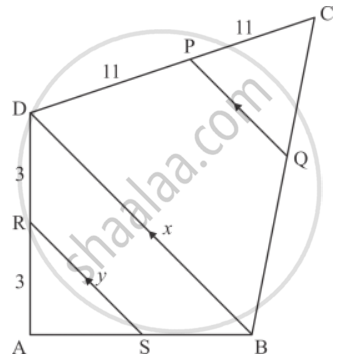
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
