Advertisements
Advertisements
Question
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
Solution
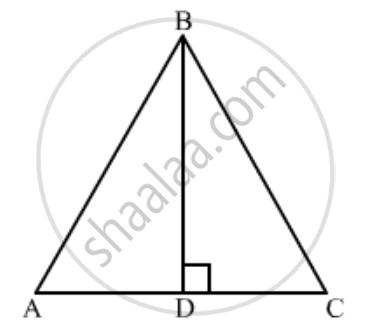
Since Δ ADB is right triangle right angled at D
`AB^2=AD^2+BD^2`
Substitute `AB=AC`
`AC^2 =AD^2+BD^2`
`AC^2=(AC-DC)^2+BD^2`
`AC^2=AC^2+DC^2-2AC.DC+BD^2`
`2AC.DC=AC^2-AC^2+DC^2+BD^2`
`2AC.DC=DC^2+BD^2`
Now, in Δ BDC, we have
`CD^2+BD^2=BC^2`
Therefore , `2AC.DC = DC^2+BD^2`
`2AC.DC=BC^2`
Hence proved.
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
