Advertisements
Advertisements
Question
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
Solution
Given: In Δ ABC ray AD bisects angle A and intersects BC in D, If `BC = a, AC=b` and `AB =c`
To Prove:
The corresponding figure is as follows
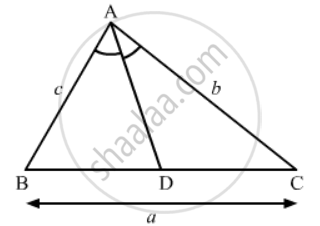
Proof: In triangle ABC, AD is the bisector of `∠ A`
Therefore `(AB)/(AC)=(BD)/(CD)`
Substitute `BC = a, AC= b` and `AB =c` we get,
`c/b=(BD)/(BC-BD)`
`c/b=(BD)/(a-BD)`
By cross multiplication we get.
`c(a-BD)=bxxBD`
`ac-cBD=bBD`
`ac=bBD+cBD`
`ac=(b+2)BD`
`(ac)/(b+c)=BD`
We proved that `BD=(ac)/(b+c)`
APPEARS IN
RELATED QUESTIONS
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
