Advertisements
Advertisements
Question
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
Options
∆FDE ∼ ∆CAB
∆FDE ∼ ∆ABC
∆CBA ∼ ∆FDE
∆BCA ∼ ∆FDE
Solution
We know that if two triangles are similar if their corresponding sides are proportional.

It is given that ΔABC and ΔDEF are two triangles such that
`(AB)/(DE)=(BC)/(EF)=(CA)/(FD)`.
\[\angle A = \angle D\]
\[\angle B = \angle E\]
\[\angle C = \angle F\]
∴ ΔCAB ∼ ΔFDE
Hence the correct answer is `a`.
APPEARS IN
RELATED QUESTIONS
In below figure, If AB || CD, find the value of x.
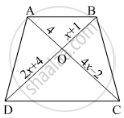
In the below figure, If AB || CD, find the value of x.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In the given figure, DE || BD. Determine AC and AE.

In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
