Advertisements
Advertisements
Question
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution
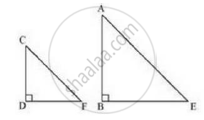
Let AB be a tower
CD be a stick, CD = 6m
Shadow of AB is BE = 28m
Shadow of CD is DF = 4m
At same time light rays from sun will fall on tower and stick at same angle.
So, ∠DCF = ∠BAE
And ∠DFC = ∠BEA
∠CDF = ∠ABE (tower and stick are vertical to ground)
Therefore Δ ABE ~ ΔCDF (By AA similarity)
So,
`"AB"/"CD"="BE"/"DF"`
`"AB"/6=28/4`
`"AB"=28xx6/4=42` m
So, height of tower will be 42 metres.
APPEARS IN
RELATED QUESTIONS
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
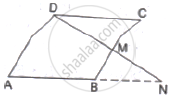
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
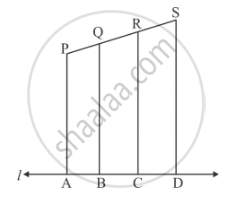
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
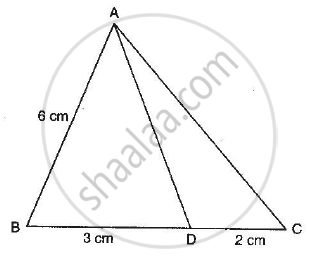
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
In the given figure the measure of ∠D and ∠F are respectively
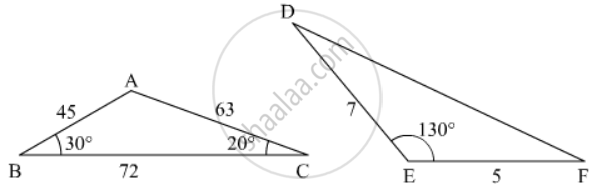
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
