Advertisements
Advertisements
Question
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
Options
BC = CY
BC = BY
BC ≠ CY
BC ≠ BY
Solution
Given: XY||BC and BY is bisector of
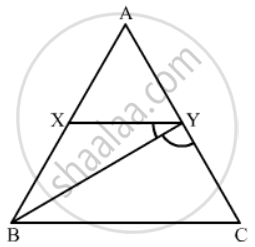
Since XY||BC
So
Now, in triangle BYC two angles are equal. Therefore, the two corresponding sides will be equal.
Hence, BC = CY
Hence option (a) is correct.
APPEARS IN
RELATED QUESTIONS
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
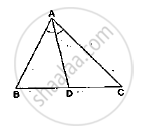
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

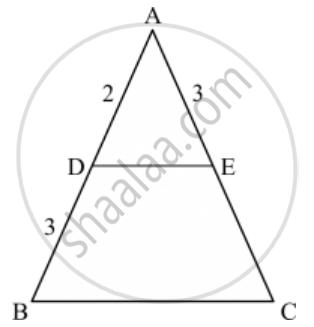
In the given figure, DE || BD. Determine AC and AE.

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

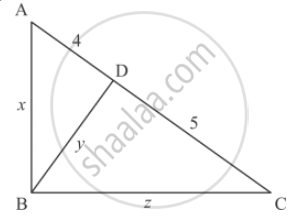
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

In the given figure, if ∠ADE = ∠ABC, then CE =