Advertisements
Advertisements
Question
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

Solution
In two triangle, we observe that
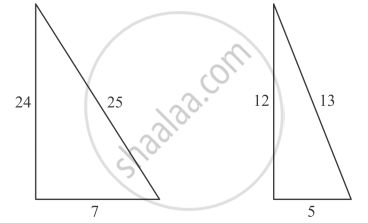
`24/12cancel=25/13cancel=7/5`
In two triangles corresponding sides are not proportional to each other.
No two triangles are not similar.
APPEARS IN
RELATED QUESTIONS
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

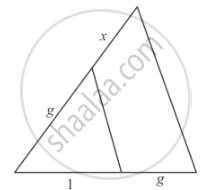
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
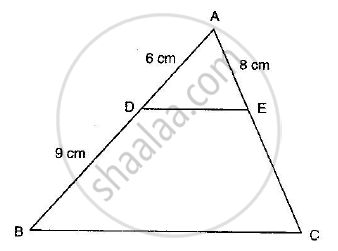
In the adjoining figure, find AC.
State SSS similarity criterion.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
