Advertisements
Advertisements
Question
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
Solution
Given: ΔABC where ∠C is an obtuse angle, AD ⊥ BC and AB2 = AC2 + 3BC2

To prove: BC = CD
Proof:
In ΔABC, ∠C is obtuse.
Therefore,
AB2 = AC2 + BC2 + 2BC × DC (Obtuse angle theorem) …(1)
AB2 = AC2 + 3BC2 (Given) …(2)
From (1) and (2), we get
AC2 + 3BC2 = AC2 + BC2 + 2BC × DC
⇒ 3BC2 = BC2 + 2BC × DC
⇒ 2BC2 = 2BC × DC
⇒ BC = DC
APPEARS IN
RELATED QUESTIONS
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

In below figure, If AB || CD, find the value of x.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
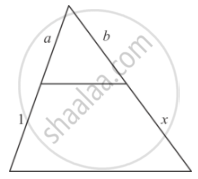
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
