Advertisements
Advertisements
Question
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
Options
4 : 5
5 : 4
3 : 2
5 : 7
Solution
Given: Two isosceles triangles have equal vertical angles and their areas are in the ratio of 16:25.
To find: Ratio of their corresponding heights.
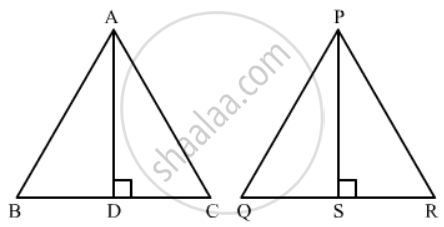
Let ∆ABC and ∆PQR be two isosceles triangles such that
\[\angle A = \angle P\]
\[ \therefore ∆ ABC~ ∆ PQR \left( SAS similarity \right)\]
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
Hence,
\[\frac{Ar\left( ∆ ABC \right)}{Ar\left( ∆ PQR \right)} = \left( \frac{AD}{PS} \right)^2 \]
\[ \Rightarrow \frac{16}{25} = \left( \frac{AD}{PS} \right)^2 \]
\[ \Rightarrow \frac{AD}{PS} = \frac{4}{5}\]
Hence we got the result as `a`
APPEARS IN
RELATED QUESTIONS
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
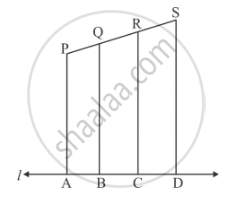
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
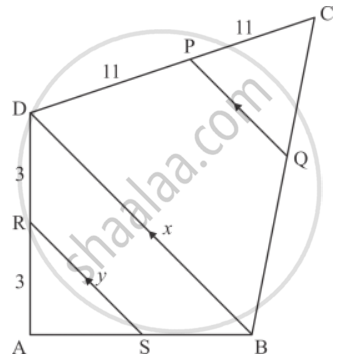
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
