Advertisements
Advertisements
Question
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
Options
30°
45°
90°
60°
Solution
Given: In Isosceles ΔABC, AC = BC and AB2 = 2AC2.
To find: Measure of angle C
In Isosceles ΔABC
AC = BC
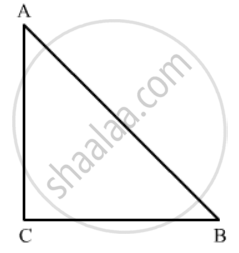
Hence the correct answer is `c`.
APPEARS IN
RELATED QUESTIONS
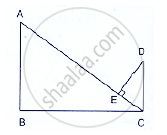
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
∆ABC ∼ ∆DEF, ar(∆ABC) = 9 cm2, ar(∆DEF) = 16 cm2. If BC = 2.1 cm, then the measure of EF is
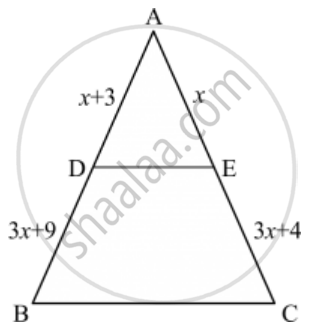
In the given figure, the value of x for which DE || AB is
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
