Advertisements
Advertisements
Question
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
Solution
Let ∆ABC and ΔPQR are similar triangles. The area of triangles is 169cm2 and 121cm2, respectively.
Longest side of the larger triangle is 26cm
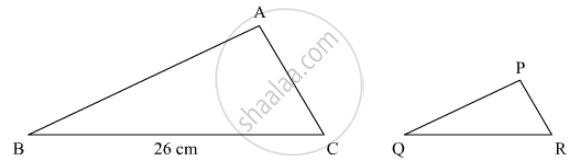
TO FIND: length of longest side of the smaller side.
Suppose longest side of the larger triangle is BC and longest side of the smaller triangle is QR.
We know that the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
Hence,
`(ar(Δ ABC))/(ar(Δ PQR))=(BC^2)/(QR^2)`
`169/121=26^2/(QR^2)`
`13/11=26/(QR)`
`QR=(11xx26)/13`
`QR=22`
`QR= 22cm`
APPEARS IN
RELATED QUESTIONS
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

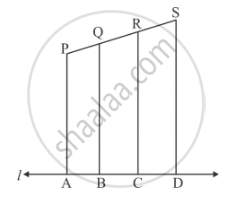
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
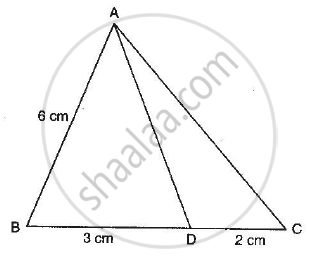
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
State SAS similarity criterion.
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
In the given figure, Δ AHK ∼ Δ ABC. If AK = 8 cm, BC = 3.2 cm and HK = 6.4 cm, then find the length of AC.

