Advertisements
Advertisements
Question
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
Solution
Given: In Δ ABC, D and E are points on sides AB and AC such that `ADxxECxxAExxDB`
To Prove: DE||BC
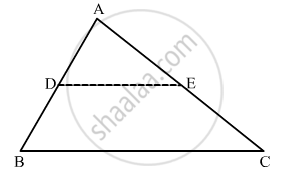
Proof:
Since `ADxxECxxAExxDB`
`⇒ (DB)/(AD)=(EC)/(AE)`
`⇒ (DB)/(AD)+1=(EC)/(AE)+1`
`⇒ (DB+AD)/(AD)=(EC+AE)/(AE)`
`⇒ (AB)/(AD)=(AC)/(AE)`
∴ DE || BC (Converse of basic proportionality theorem)
APPEARS IN
RELATED QUESTIONS
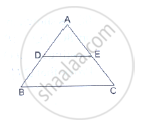
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
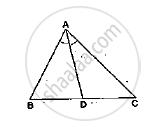
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
State Pythagoras theorem and its converse.
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
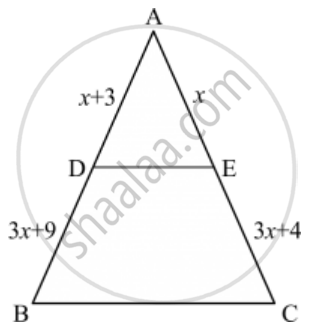
In the given figure, the value of x for which DE || AB is