Advertisements
Advertisements
प्रश्न
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
उत्तर
Given: In Δ ABC, D and E are points on sides AB and AC such that `ADxxECxxAExxDB`
To Prove: DE||BC
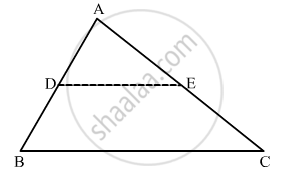
Proof:
Since `ADxxECxxAExxDB`
`⇒ (DB)/(AD)=(EC)/(AE)`
`⇒ (DB)/(AD)+1=(EC)/(AE)+1`
`⇒ (DB+AD)/(AD)=(EC+AE)/(AE)`
`⇒ (AB)/(AD)=(AC)/(AE)`
∴ DE || BC (Converse of basic proportionality theorem)
APPEARS IN
संबंधित प्रश्न
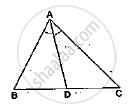
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
What values of x will make DE || AB in the given figure?

In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
State SAS similarity criterion.
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
