Advertisements
Advertisements
प्रश्न
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
पर्याय
CD2
2CD2
3CD2
4CD2
उत्तर
In an equilateral ΔABC, `AD ⊥ BC`.
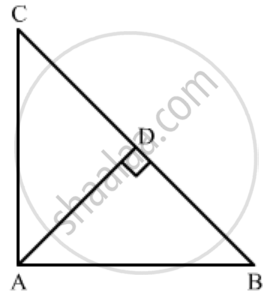
In ΔADC, applying Pythagoras theorem, we get
`AC^2=AD^2+DC^2`
`BC^2=AD^2+DC^2(∵ AC=BC)`
`(2DC)^2=AD^2+DC^2(∵ BC=2DC)`
`4DC^2=AD^2+DC^2`
`3DC^2=AD^2`
Hence, the correct option is (c).
APPEARS IN
संबंधित प्रश्न
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
