Advertisements
Advertisements
प्रश्न
In an equilateral triangle ABC if AD ⊥ BC, then
पर्याय
5AB2 = 4AD2
3AB2 = 4AD2
4AB2 = 3AD2
2AB2 = 3AD2
उत्तर
∆ABC is an equilateral triangle and `AD ⊥ BC`.
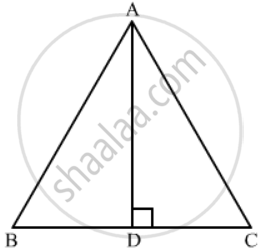
In ∆ABD, applying Pythagoras theorem, we get
`AB^2=AD^2+BD^2`
`AB^2=AD^2+(1/2BC)^2(∵BD=1/2BC)`
`AB^2=AD^2+(1/2AB)^2(∵ AB=BC)`
`AB^2=AD^2+1/2AB^2`
`3AB^2=4AD^2`
We got the result as `b`.
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
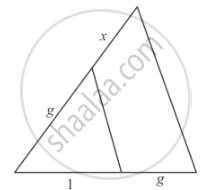
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
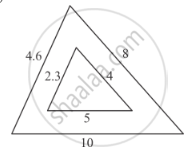
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
