Advertisements
Advertisements
Question
In an equilateral triangle ABC if AD ⊥ BC, then
Options
5AB2 = 4AD2
3AB2 = 4AD2
4AB2 = 3AD2
2AB2 = 3AD2
Solution
∆ABC is an equilateral triangle and `AD ⊥ BC`.
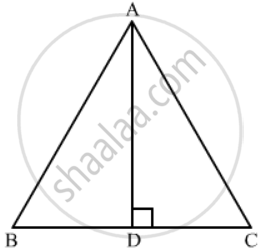
In ∆ABD, applying Pythagoras theorem, we get
`AB^2=AD^2+BD^2`
`AB^2=AD^2+(1/2BC)^2(∵BD=1/2BC)`
`AB^2=AD^2+(1/2AB)^2(∵ AB=BC)`
`AB^2=AD^2+1/2AB^2`
`3AB^2=4AD^2`
We got the result as `b`.
APPEARS IN
RELATED QUESTIONS
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
