Advertisements
Advertisements
प्रश्न
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
उत्तर
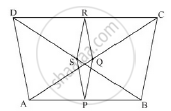
AD = BC and P, Q, R and S are the mid-points of sides AB, AC, CD and BD respectively, show that PQRS is a rhombus.
In ΔBAD, by mid-point theorem
PS || AD and PS `=1/2` AD .......(i)
In ΔCAD, by mid-point theorem
QR || AD and QR `=1/2` AD .......(ii)
Compare (i) and (ii)
PS || QR and PS = QR
Since one pair of opposite sides is equal as well as parallel then
PQRS is a parallelogram ...(iii)
Now, In ΔABC, by mid-point theorem
PQ || BC and PQ `=1/2` BC .......(iv)
And, AD = BC …(v) [given]
Compare equations (i) (iv) and (v)
PS = PQ …(vi)
From (iii) and (vi)
Since, PQRS is a parallelogram with PS = PQ then PQRS is a rhombus.
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

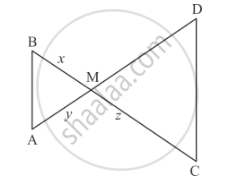
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
