Advertisements
Advertisements
प्रश्न
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
उत्तर
GIVEN: the lengths of the diagonals of a rhombus are 30 cm and 40 cm.
TO FIND: side of the rhombus.
Let the diagonals AC and CD of the rhombus ABCD meet at point O.
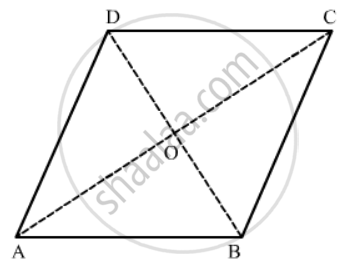
We know that the diagonals of the rhombus bisect each other perpendicularly.
Hence in right triangle AOD, by Pythagoras theorem
`\text{hypotenuse}^2+\text{perpendicular}^2+\text{base}^2`
`=15^2+20^2`
`=225+400`
`=625`
`\text{hypotenuse}=25 cm`
Hence the side of the rhombus is = 25 cm
APPEARS IN
संबंधित प्रश्न
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2 then prove that ∠ACD = 90°.
State AAA similarity criterion.
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
