Advertisements
Advertisements
Question
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
Solution
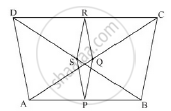
AD = BC and P, Q, R and S are the mid-points of sides AB, AC, CD and BD respectively, show that PQRS is a rhombus.
In ΔBAD, by mid-point theorem
PS || AD and PS `=1/2` AD .......(i)
In ΔCAD, by mid-point theorem
QR || AD and QR `=1/2` AD .......(ii)
Compare (i) and (ii)
PS || QR and PS = QR
Since one pair of opposite sides is equal as well as parallel then
PQRS is a parallelogram ...(iii)
Now, In ΔABC, by mid-point theorem
PQ || BC and PQ `=1/2` BC .......(iv)
And, AD = BC …(v) [given]
Compare equations (i) (iv) and (v)
PS = PQ …(vi)
From (iii) and (vi)
Since, PQRS is a parallelogram with PS = PQ then PQRS is a rhombus.
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In the given figure, DE || BD. Determine AC and AE.

In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
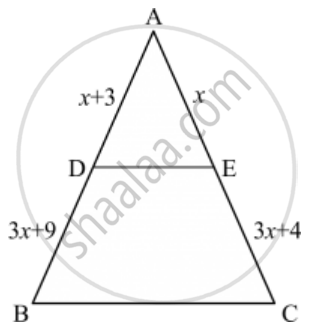
In the given figure, the value of x for which DE || AB is
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
