Advertisements
Advertisements
Question
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
Solution
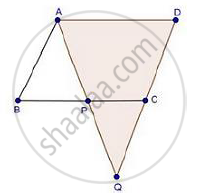
Given: ABCD is a parallelogram
To prove: BP × DQ = AB × BC
Proof: In ΔABP and ΔQDA
∠B = ∠D [Opposite angles of parallelogram]
∠BAP = ∠AQD [Alternate interior angles]
Then, ΔABP ~ ΔQDA [By AA similarity]
`therefore"AB"/"QD"="BP"/"DA"` [Corresponding parts of similar Δ are proportional]
But, DA = BC [Opposite sides of parallelogram]
Then, `therefore"AB"/"QD"="BP"/"BC"`
⇒ AB × BC = QD × BP
APPEARS IN
RELATED QUESTIONS
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
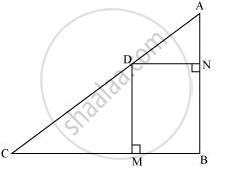
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
State the AAA-similarity criterion
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.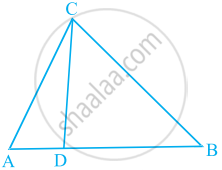
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.
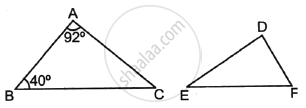
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?