Advertisements
Advertisements
Question
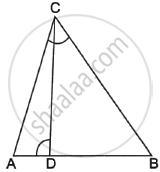
In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.
Solution
Given, AC = 8 cm, AD = 3 cm
and ∠ADC = ∠BCA
From the figure in ΔADC and ΔBCA
∠A = ∠A ...(Common)
∠ADC = ∠BCA ...(Given)
So, by AA similarity criteria
ΔADC ∼ ΔBCA
∵ Corresponding sides are in the same ratio
`(AC)/(AD) = (AB)/(AC)`
`8/3 = (AB)/8`
AB = `(8 xx 8)/3`
= `64/3` cm
Now from the figure,
BD = AB – AD
= `64/3 - 3`
= `(64 - 9)/3`
= `55/3`
BD = `18 1/3` cm.
APPEARS IN
RELATED QUESTIONS
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
In the following figure, AB || QR. Find the length of PB.

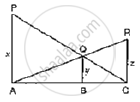
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
In the given figure, value of x(in cm) is

Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
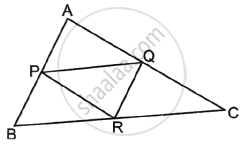
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
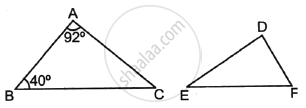
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?