Advertisements
Advertisements
Question
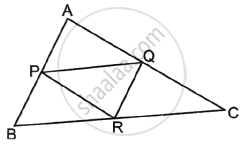
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
Solution
Given: ABC is a triangle and P, Q and R are the midpoints of sides AB, AC, and BC, respectively.
To prove: ΔABC is divided into 4 congruent triangles.
Proof: P and Q are the mid-points of AB and AC of ΔABC.
So, PQ || BC ......[Line segment joining the mid-points of two sides of a triangle is parallel to the third side]
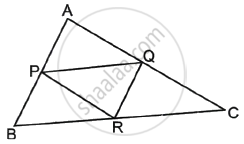
Similarly, PR || AC and QR || AB
In PQRB, PB || QR and PQ || BR ......[Parts of parallel lines are parallel]
i.e., Both opposite pairs of sides are parallel.
As a result, PQRB is a parallelogram.
As a result, PR is a diagonal of the parallelogram PQRB.
So, ΔPBR ≅ ΔPQR .....[A diagonal of a parallelogram divides it into two congruent triangles.] .....(i)
APRQ is also a parallelogram.
So, ΔAPQ ≅ ΔPQR .....(ii)
PQRC is also a parallelogram.
So, ΔPQR ≅ ΔQRC ......(iii)
From equations (i), (ii) and (iii),
ΔPBR ≅ ΔPQR ≅ ΔAPQ ≅ ΔQRC
As a result, all four triangles are congruent.
Hence Proved.
APPEARS IN
RELATED QUESTIONS
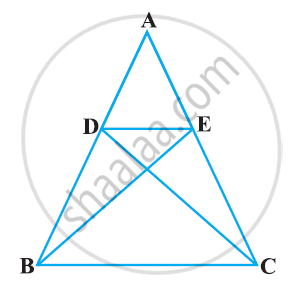
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii) `"OA"/"OC"="OM"/"OL"`
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
In the given figure MN|| BC and AM: MB= 1: 2
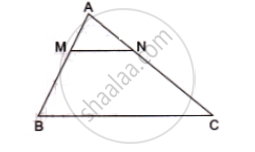
find ` (area(ΔAMN))/(area(ΔABC))`
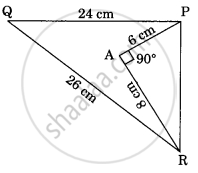
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?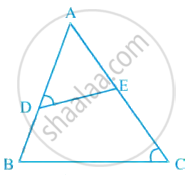
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

