Advertisements
Advertisements
Question
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

Solution
In ΔABC,
∠1 = ∠2
∴ AB = BD ......(i)
Given, `(AD)/(AE) = (AC)/(BD)`
Using equation (i), we get
`(AD)/(AE) = (AC)/(AB)` ......(ii)
In ΔBAE and ΔCAD, by equation (ii),
`(AC)/(AB) = (AD)/(AE)`
∠A = ∠A ......(Common)
∴ ΔBAE ∼ ΔCAD ......[By SAS similarity criterion]
APPEARS IN
RELATED QUESTIONS
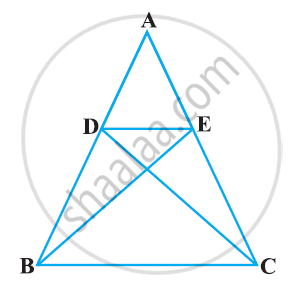
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
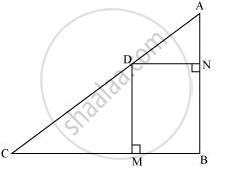
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
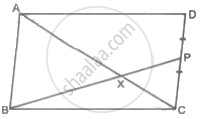
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
In the given figure, ΔLMN is similar to ΔPQR. To find the measure of ∠N, complete the following activity.
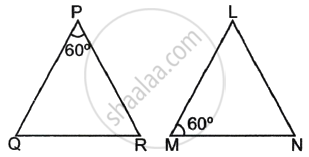
Given: ΔLMN ∼ ΔPQR
Since ΔLMN ∼ ΔPQR, therefore, corresponding angles are equal.
So, ∠L ≅ `square`
⇒ ∠L = `square`
We know, the sum of angles of a triangle = `square`
∴ ∠L + ∠M + ∠N = `square`
Substituting the values of ∠L and ∠M in equation (i),
`square` + `square` + ∠N = `square`
∠N + `square` = `square`
∠N = `square` – `square`
∠N = `square`
Hence, the measure of ∠N is `square`.
