Advertisements
Advertisements
Question
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Solution

Let AB be A ladder and B is the window at 8 m above the ground C.
Now, In right triangle ABC
By using Pythagoras theorem, we have
`AB^2=BC^2+CA^2`
⇒ `10^2=8^2+CA^2`
⇒ `CA^2=100-64`
⇒ `CA^2=36`
⇒` CA=6m`
Hence, the distance of the foot of the ladder from the base of the wall is 6 m.
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
In the following figure, AB || QR. Find the length of PB.

In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

State the AAA-similarity criterion
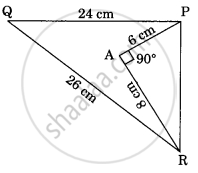
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?