Advertisements
Advertisements
Question
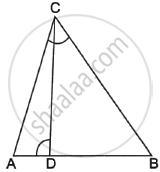
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

Solution
We have, ∠ABC = 90° and BD ⊥ AC
Now, ∠ABD + ∠DBC − 90° …(i) [∵ ∠ABC − 90°]
And, ∠C + ∠DBC − 90° …(ii) [By angle sum prop. in ΔBCD]
Compare equations (i) & (ii)
∠ABD = ∠C …(iii)
In ΔABD and ΔBCD
∠ABD = ∠C [From (iii)]
∠ADB = ∠BDC [Each 90°]
Then, ΔABD ~ ΔBCD [By AA similarity]
`therefore"BD"/"CD"="AD"/"BD"` [Corresponding parts of similar Δ are proportional]
`rArr8/"CD"=4/8`
`rArr"CD"=(8xx8)/4=16` cm
APPEARS IN
RELATED QUESTIONS
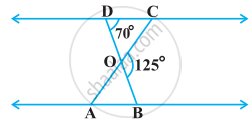
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
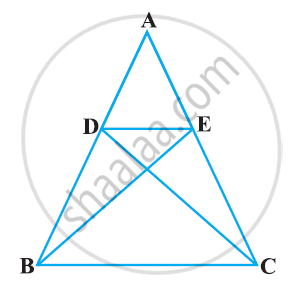
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.