Advertisements
Advertisements
Question
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
Options
`("EF")/("PR") = ("DF")/("PQ")`
`("DE")/("PQ") = ("EF")/("RP")`
`("DE")/("QR") = ("DF")/("PQ")`
`("EF")/("RP") = ("DE")/("QR")`
Solution
`bb((DE)/(PQ) = (EF)/(RP))`
Explanation:
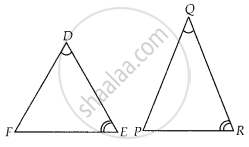
Given, in ∆DEF and ∆PQR,
∠D = ∠Q,
∠R = ∠E
∴ ∆DEF ~ ∆QRP ...[By AAA similarity criterion]
⇒ ∠F = ∠P ...[Corresponding angles of similar triangles]
∴ `("DF")/("QP") = ("ED")/("RQ") = ("FE")/("PR")`
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
In the given figure, value of x(in cm) is

D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).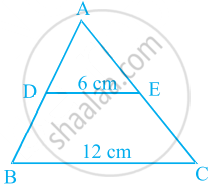
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
