Advertisements
Advertisements
Question
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
Solution
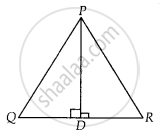
In ΔPQD and ΔRPD,
PD = PD ...[Common side]
∠PDQ = ∠PDR ...[Each 90°]
Here, no other sides or angles are equal, so we can say that ∠PQD is not similar to ΔRPD.
But, if ∠P = 90°, then ∠DPQ = ∠PRD
[Each equal to 90° – ∠0 and by ASA similarity criterion, ΔPQD ~ΔRPD]
APPEARS IN
RELATED QUESTIONS
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
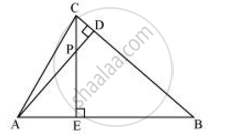
ΔAEP ∼ ΔCDP
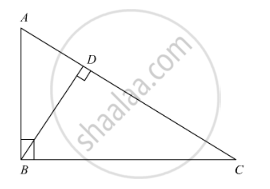
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
The sides of certain triangles are given below. Determine which of them right triangles are.
1.6cm, 3.8cm, 4cm
State the two properties which are necessary for given two triangles to be similar.
Which of the following conditions is not sufficient to determine the congruence of two triangles?
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

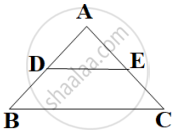
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
Which of the following is NOT a similarity criterion of traingles?
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
