Advertisements
Advertisements
Question
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

Solution
Given: Chord PQ || tangent AB
∴ ∠Q = ∠QDB = 50° ......[Alternate interior angles]
And ∠CDB = ∠PRD ......[Alternate interior angles]
ADB is a tangent at point D and CD is the circle's radius.
Thus, ∠CDB = 90° ......[Tangent theorem]
⇒ ∠CDQ + ∠QDB = 90°
⇒ ∠CDQ + 50° = 90°
⇒ ∠CDQ = 90° – 50° = 40°
CR is a perpendicular to the chord PQ, so it bisects PQ.
Thus, ∠PRC = 90° and PR = QR
Now, in ΔDRP and ΔDRQ
PR ≅ QR .....[Proved above]
∠DRP ≅ ∠DRQ ......[Each 90°]
DR ≅ DR ......[Common side]
Thus ΔDRP ≅ ΔDRQ .....[By SAS criterion of congruence)
So, ∠P ≅ ∠Q .....[C.A.C.T.]
⇒ ∠P = 50° .....[∵ ∠Q = 50°]
Now, the sum of the interior angles in a triangle is 180°.
Thus, ∠P + ∠PRD + ∠RDP = 180°
50° + 90° + ∠RDP = 180°
∠RDP = 180° – 50° – 90° = 40°
Now, ∠PDQ = ∠RDP + ∠RDQ
⇒ ∠PDQ = 40° + 40° = 80°
Hence, ∠PDQ = 80°.
APPEARS IN
RELATED QUESTIONS
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
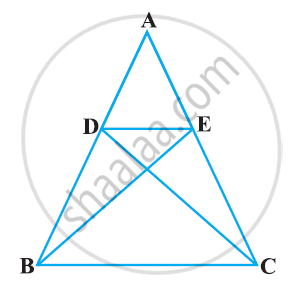
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
State the two properties which are necessary for given two triangles to be similar.
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
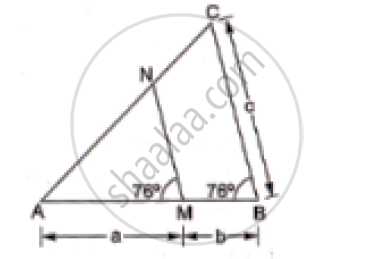
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).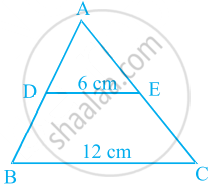
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.
Which of the following is NOT a similarity criterion of traingles?
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.
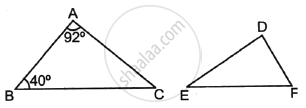
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?