Advertisements
Advertisements
Question
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
Solution
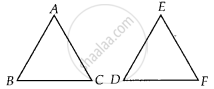
Given,
∆ABC ∼ ∆EDF,
So the corresponding sides of ∆ABC and ∆EDF are in the same ratio.
i.e., `("AB")/("ED") = ("AC")/("EF") = ("BC")/("DF")` ...(i)
Also,
AB = 5 cm,
AC = 7 cm,
DF = 15 cm
And DE = 12 cm
On putting these values in equation (i), we get
`5/12 = 7/("EF") = ("BC")/15`
On taking first and second terms, we get
`5/12 = 7/("EF")`
⇒ EF = `(7 xx 12)/5` = 16.8 cm
On taking first and third terms, we get
`5/12 = ("BC")/15`
⇒ BC = `(5 xx 15)/12` = 6.25 cm
Hence, lengths of the remaining sides of the triangles are EF = 16.8 cm and BC = 6.25 cm.
APPEARS IN
RELATED QUESTIONS
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
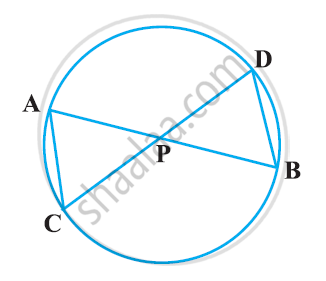
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).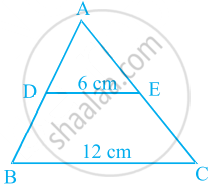
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

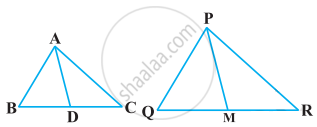
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.