Advertisements
Advertisements
प्रश्न
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
उत्तर
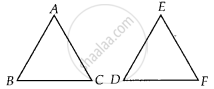
Given,
∆ABC ∼ ∆EDF,
So the corresponding sides of ∆ABC and ∆EDF are in the same ratio.
i.e., `("AB")/("ED") = ("AC")/("EF") = ("BC")/("DF")` ...(i)
Also,
AB = 5 cm,
AC = 7 cm,
DF = 15 cm
And DE = 12 cm
On putting these values in equation (i), we get
`5/12 = 7/("EF") = ("BC")/15`
On taking first and second terms, we get
`5/12 = 7/("EF")`
⇒ EF = `(7 xx 12)/5` = 16.8 cm
On taking first and third terms, we get
`5/12 = ("BC")/15`
⇒ BC = `(5 xx 15)/12` = 6.25 cm
Hence, lengths of the remaining sides of the triangles are EF = 16.8 cm and BC = 6.25 cm.
APPEARS IN
संबंधित प्रश्न
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
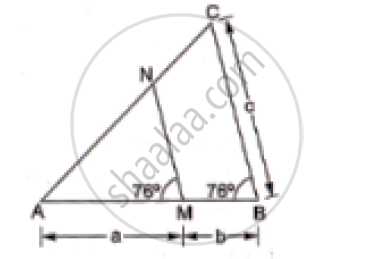
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
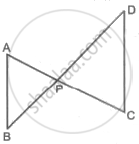
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

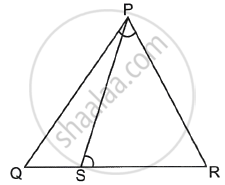
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
