Advertisements
Advertisements
Question
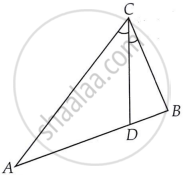
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
Solution
 |
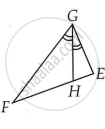 |
Given:
(i) ΔABC ∼ ΔFEG
∠A = ∠F ...(1)
∠B = ∠E ...(2)
∠C = ∠G ...(3)
The sides opposite to equal angles are essentially equal.
`"CD"/"GH" = "AC"/"FG"`
(ii) In ΔDCB and ΔHGE
In equation (2),
∠B = ∠E
In equation (3),
∠C = ∠G
∠BCD = ∠EGH
AA by similarity criterion
∆DCB ∼ ∆HGE
(iii) In ΔDCA and ΔHGF
In Equation (1)
∠A = ∠F
In equation (3),
∠C = ∠G
∠ACD = ∠FGH
AA by similarity criterion
∆DCA ∼ ∆HGF
APPEARS IN
RELATED QUESTIONS
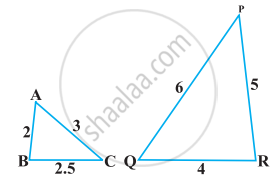
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
State the two properties which are necessary for given two triangles to be similar.
Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.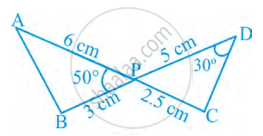
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?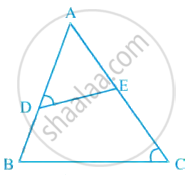
The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
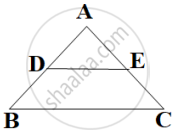
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
