Advertisements
Advertisements
Question
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
Solution
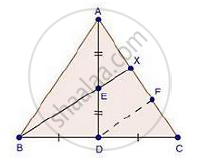
Given: In ΔABC, D is the mid-point of BC and E is the mid-point of AD.
To prove: BE : EX = 3 : 1
Const: Through D, draw DF || BX
Proof: In ΔEAX and ΔADF
∠EAX = ∠ADF [Common]
∠AXE = ∠DAF [Corresponding angles]
Then, ΔAEX ~ ΔADF [By AA similarity]
`therefore"EX"/"DF"="AE"/"AD"` [Corresponding parts of similar Δ are proportional]
`rArr"EX"/"DF"="AE"/"2AE"` [AE = ED given]
⇒ DF = 2EX …. (i)
In ΔCDF and ΔCBX [By AA similarity]
`therefore"CD"/"CB"="DF"/"BX"` [Corresponding parts of similar Δ are proportional]
`rArr1/2="DF"/"BE + EX"` [BD = DC given]
⇒ BE + EX = 2DF
⇒ BE + EX = 4EX
⇒ BE = 4EX – EX [By using (i)]
⇒ BE = 4EX – EX
`rArr"BE"/"EX"=3/1`
APPEARS IN
RELATED QUESTIONS
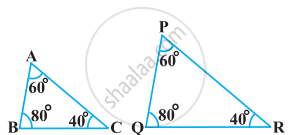
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
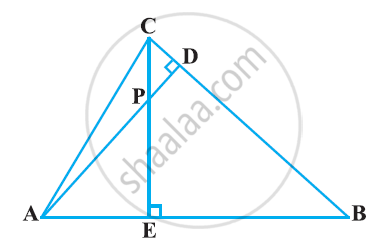
ΔAEP ∼ ΔADB
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
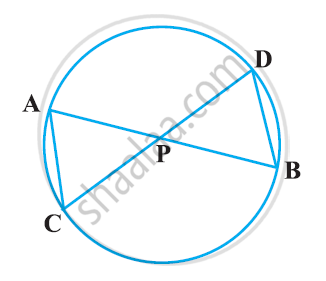
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii) `"OA"/"OC"="OM"/"OL"`
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
