Advertisements
Advertisements
प्रश्न
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
उत्तर
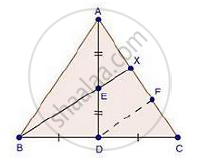
Given: In ΔABC, D is the mid-point of BC and E is the mid-point of AD.
To prove: BE : EX = 3 : 1
Const: Through D, draw DF || BX
Proof: In ΔEAX and ΔADF
∠EAX = ∠ADF [Common]
∠AXE = ∠DAF [Corresponding angles]
Then, ΔAEX ~ ΔADF [By AA similarity]
`therefore"EX"/"DF"="AE"/"AD"` [Corresponding parts of similar Δ are proportional]
`rArr"EX"/"DF"="AE"/"2AE"` [AE = ED given]
⇒ DF = 2EX …. (i)
In ΔCDF and ΔCBX [By AA similarity]
`therefore"CD"/"CB"="DF"/"BX"` [Corresponding parts of similar Δ are proportional]
`rArr1/2="DF"/"BE + EX"` [BD = DC given]
⇒ BE + EX = 2DF
⇒ BE + EX = 4EX
⇒ BE = 4EX – EX [By using (i)]
⇒ BE = 4EX – EX
`rArr"BE"/"EX"=3/1`
APPEARS IN
संबंधित प्रश्न
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
In the following figure, AB || QR. Find the length of PB.

ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
