Advertisements
Advertisements
प्रश्न
In the following figure, AB || QR. Find the length of PB.

उत्तर
We have, ΔPAB and ΔPQR
∠P = ∠P [common]
∠PAB = ∠PQR [corresponding angles]
Then, ΔPAB ~ ΔPQR [By AA similarity]
`therefore"PB"/"PR"="AB"/"QR"` [Corresponding parts of similar Δare proportional]
`rArr"PB"/6=3/9`
`rArr"PB"=3/9xx6=2` cm
APPEARS IN
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

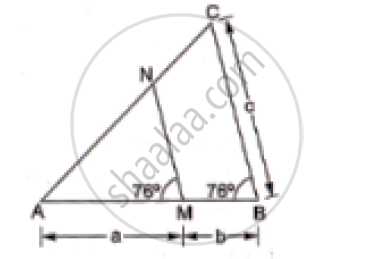
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
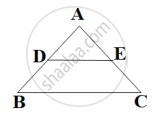
In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
