Advertisements
Advertisements
प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
उत्तर
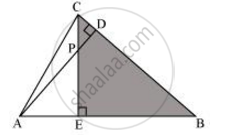
In ΔPDC and ΔBEC
∠PDC = ∠BEC = 90°
∠PCD = ∠BCE ...(Common angle)
Hence, by using the AA similarity criterion,
ΔPDC ∼ ΔBEC
संबंधित प्रश्न
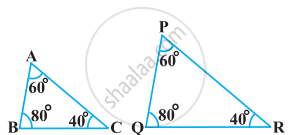
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
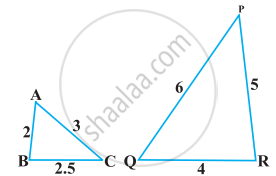
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
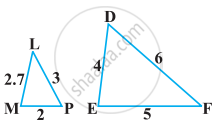
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
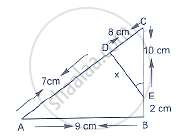
In below figure, ∠A = ∠CED, Prove that ΔCAB ~ ΔCED. Also, find the value of x.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
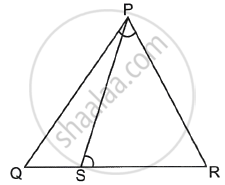
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
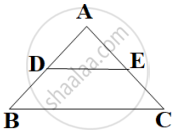
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
