Advertisements
Advertisements
प्रश्न
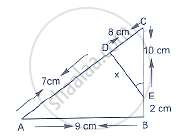
In below figure, ∠A = ∠CED, Prove that ΔCAB ~ ΔCED. Also, find the value of x.
उत्तर
We have, ∠A = ∠CED
In ΔCAB and ΔCED
∠C = ∠C [Common]
∠A = ∠CED [Given]
Then, ΔCAB ~ ΔCED [By AA similarity]
`therefore"CA"/"CE"="AB"/"ED"` [Corresponding parts of similar Δ are proportional]
`rArr15/10=9/x`
`rArrx=(10xx9)/15=90/15=6 ` cm
APPEARS IN
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
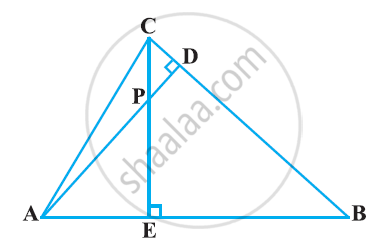
ΔAEP ∼ ΔADB
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
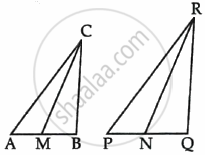
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.
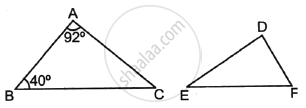
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
