Advertisements
Advertisements
प्रश्न
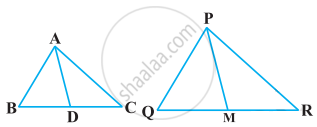
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
उत्तर १
(i) In ΔABC and ΔAMP,
∠ABC = ∠AMP ...(Each 90°)
∠A = ∠A ...(Common)
∴ ΔABC ∼ ΔAMP ...(By AA similarity criterion)
(ii) We have,
∠B = ∠M = 90°
And, ∠BAC = ∠MAP
In ΔABC and ΔAMP
∠B = ∠M ...[Each 90°]
∠BAC = ∠MAP ...[Given]
Then, ΔABC ~ ΔAMP ....[By AA similarity]
∴ `"CA"/"PA"="BC"/"MP"` ....[Corresponding parts of similar Δ are proportional.]
उत्तर २
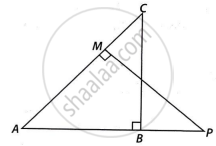
We have,
∠B = ∠M = 90°
And, ∠BAC = ∠MAP
In ΔABC and ΔAMP
∠B = ∠M ...[Each 90°]
∠BAC = ∠MAP ...[Given]
Then, ΔABC ~ ΔAMP ...[By AA similarity]
∴ `"CA"/"PA"="BC"/"MP"` ....[Corresponding parts of similar Δ are proportional]
APPEARS IN
संबंधित प्रश्न
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
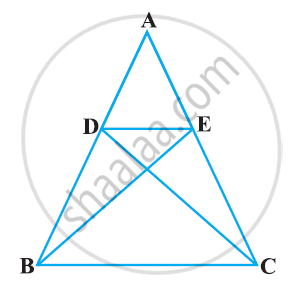
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
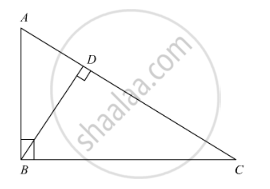
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

State the two properties which are necessary for given two triangles to be similar.
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?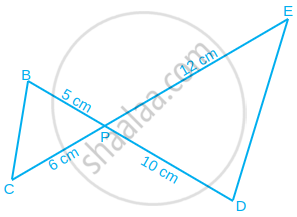
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.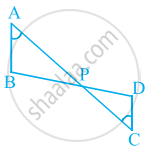
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.